An extraordinarily deep understanding of mathematics.
What do I need to demonstrate the Riemann hypothesis?
What is the square root of 4,761?
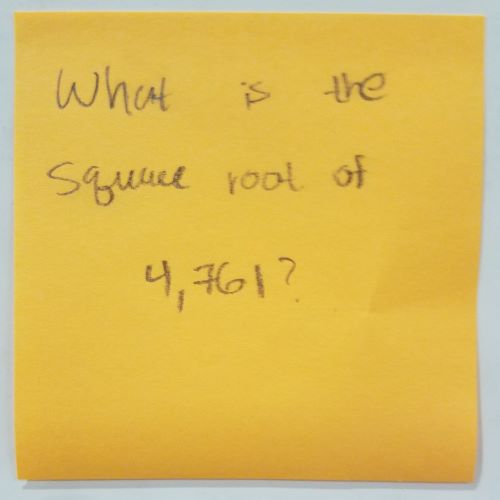
Unless this is a trick question, the square root of 4,761 is 69.
Solve Ψ
![[Quantum mechanics equation] Solve Ψ](https://library.bc.edu/answerwall/wp-content/uploads/2019/11/aw112719-1.jpg)
You’re setting the (h-)bar really high. I may be reduced to walking the Planck and sinking into the wave function.
Is the derivative or the integral of your life more important?
I’d say both, but in different ways. A derivative is going to tell you about what’s going on at a particular moment, and it’s important to live in the moment. But the whole area under the curve of your life is also important to show you the big picture. The derivative may cloud your mind during rough periods (“I’m going downhill fast!”), but integrating over the course of your life (with the limits being birth and death) can reassure you that this is just a phase.
How to learn abstract math?
You could do worse than to start with Khan Academy, but there are some experts here on campus who could answer that question in depth: the Math Department: bit.ly/bc-math-dept
Sounds like this is the math version of believing 6 impossible things before breakfast?
Was math created or discovered?
Though the word “mathematics” was coined by the Pythagoreans in 6th C. BC Greece, it’s clear that wasn’t the first math. Records of arithmetic, algebra, and geometry go back much further, to areas in the near East, near modern Egypt and Iraq, and it’s quite possible forms of mathematics existed long before the printed word (or number). Here are a few dozen books on the topic: bit.ly/bc-ancient-math
Math B.S students ain’t gonna get no more social lives…
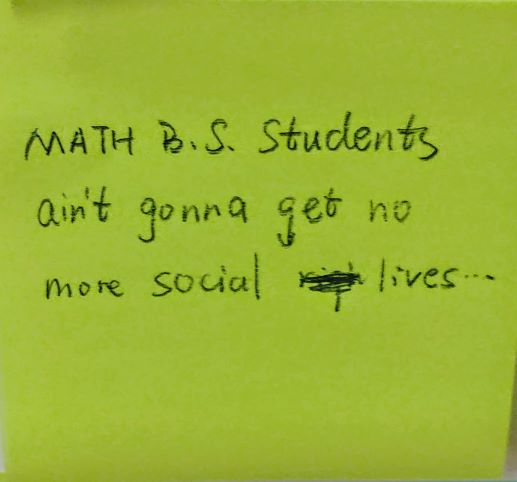
Heavy workload? Ouch. Study in groups: not only will you learn more, but you get a little social life as a bonus. (OK maybe that’s not what quite enough.) And see tutors and an academic coach at the CFLC (bit.ly/BC-connors) to help your work become more focused and efficient, which will make time for more social life. In the meantime, ugh, but you’ll get through it.
Why is Algebra so hard? :(
Multiple variables are a head-spinner for sure, and algebra starts asking you to put together a lot of different math skills & concepts to solve any single problem. I recommend working in groups and working with tutors at the CFLC: bit.ly/BC-connors. Algebra is more approachable if you talk through it rather than just try to think through it alone.
In that case, she or he has my deep sympathy.
How does math department decide which professor teach a certain course next year?
My assistants have contacted the math department; I’ll update you when they provide an answer. Update 9/20: The Math Dept. responds: “We survey the faculty as to their teaching preferences, and to the extent that we can, accommodate their preferences within the constraints of the courses we are required to offer.”
Is “parameterization” or “parametrization” correct when describing which parameters describe a statistical model?
The Oxford English Dictionary recognizes both as options (and even parameterisation, imagine that!), so you can choose the one you like. I ran a Google Trends search to see usage of the 3 spellings over the past 15 years (bit.ly/Paramewhat); “parameterization” was the clear winner.
tan(10°) + tan(20°) + tan(30°) + … + tan(80°)=?
If you meant what you asked, the answer is 13.2994. A more interesting question with that sequence would be tan(10°)* tan(20°)*tan(30°)* … * tan(80°) = ? Because tan(90°−x) = cotx = 1/tanx, tan(10°)* tan(80°) = tan(10°)*1/tan(10°) = 1. Similarly, the rest of the sequence cancels out with the final answer being 1. However, as a wall, I’m more into geometry than trigonometry – give me more than one right angle, please.
why does e^πi = -1 ?
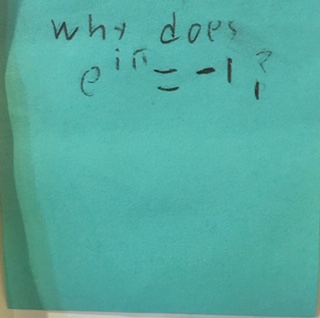
Because eπi = cos(π) + isin(π) = -1 + i(0) = -1
Why x^2-2/2y^2+3 never an integer for x,y,∈z
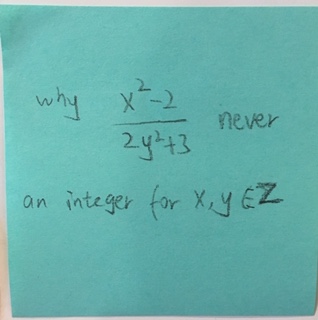
(x^2 − 2)/(2y^2 + 3) can be shown never to be an integer, when x and y are integers, using a proof by contradiction. See question 5 of this problem set for the full solution (bit.ly/contradictionproof).
What if I can’t become a mathematician
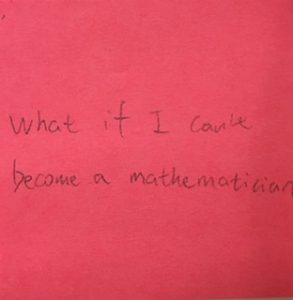
That would be sad, if it’s what your heart is set upon. On the other hand, having a math background will stand you in good stead in anything else you pursue. I recommend the MAA Career Resources Center (bit.ly/MathishCareers) and this site from UC/Irvine (bit.ly/MoreMathCareers). We also have 101 careers in mathematics (O’Neill Stacks QA10.5 .A15 2014). And consider a consultation with the BC Career Center (bit.ly/BC-career). Best of luck!
I’m a current math & econ major student, and I want to be a professor in BC in the future.
I know many things, and one thing I know is that your math and econ professors will have considerably better advice than I would about academic careers in those fields. Talk to all of them. Meanwhile, check this title: Complexities: Women in Mathematics, by Bettye Anne Case & Anne M Leggett. (O’Neill QA27.5 .C66 2005)
lim x–>0 sinx/x using Squeeze Theorem explained
Khan Academy rocks: bit.ly/KAVidLimit
What are the most promising career fields for someone studying mathematics?
See the Mathematical Association of America (MAA) Career Resources Center (bit.ly/MathishCareers) for inspiration on what to do with your math degree. Also this site has a lot of information (bit.ly/MoreMathCareers). Or check out the book 101 Careers in Mathematics (O’Neill Stacks QA10.5 .A15 2014). The great thing is that you can bring your math skills to any future path.
Is every simply connected, close 3- manifold homeomorphic to the 3-sphere? If yes, please provide proof.
Yes. Poincaré’s conjecture (formerly a Clay Mathematics Institute Millennium Prize Problem) was proved by Grigori Perelman using Richard Hamilton’s Ricci flow program and confirmed in 2006 following review (bit.ly/CMIperelsol). Read the complete proof in the Asian Journal of Mathematics (bit.ly/poincareproof).
I have a lot of math homework. What should I do? :)
![[in Chinese] I have a lot of math homework. What should I do? :)](http://library.bc.edu/answerwall/wp-content/uploads/2018/02/aw020718-6.jpg)
1. Set aside sufficient time. 2. Take it in short bursts, with rests for stretching & snacks (maybe even offer yourself rewards: if I get x # of problems done in an hour, I get a treat.) 3. Get help from a tutor in the CFLC (bit.ly/BC-connors); a firmer understanding might make the work go faster. Good luck! If you need a handy reference tool for problems that assume other knowledge, this book might help: Mastering Mathematics: How to be a Great Math Student. (O’Neill Library QA11 .S63 1994).