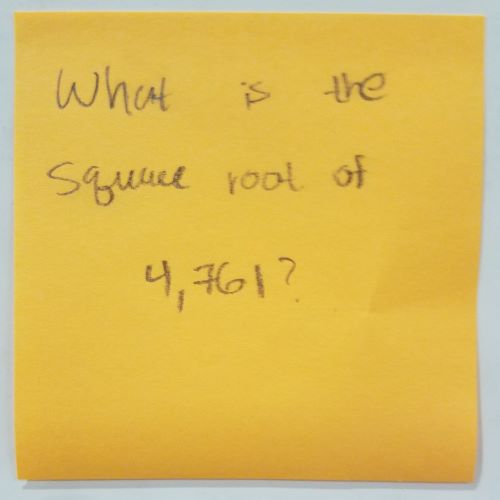
Unless this is a trick question, the square root of 4,761 is 69.

Answering questions at Boston College O’Neill Library
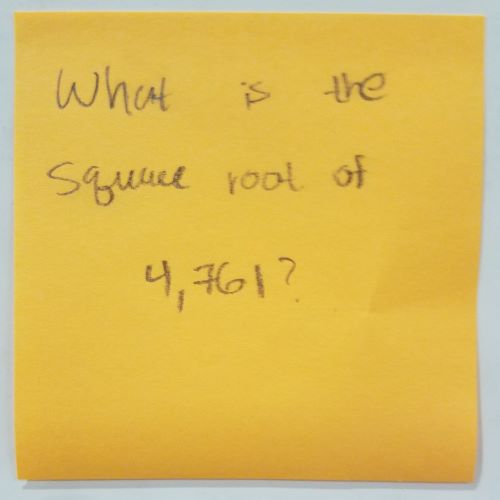
Unless this is a trick question, the square root of 4,761 is 69.

I’m sorry you’re having a bad experience in math. I doubt your teacher hates you; if you’re struggling, it’s more likely they’re feeling compassion, because teachers really do want all of their students to succeed. If you’re having difficulty, I recommend both meeting with your professor for help and meeting with tutors in the CFLC: bit.ly/BC-connors
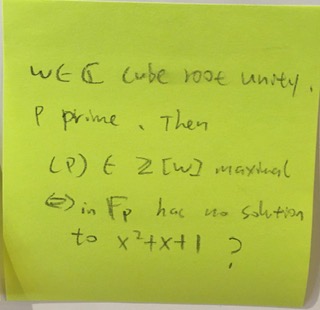
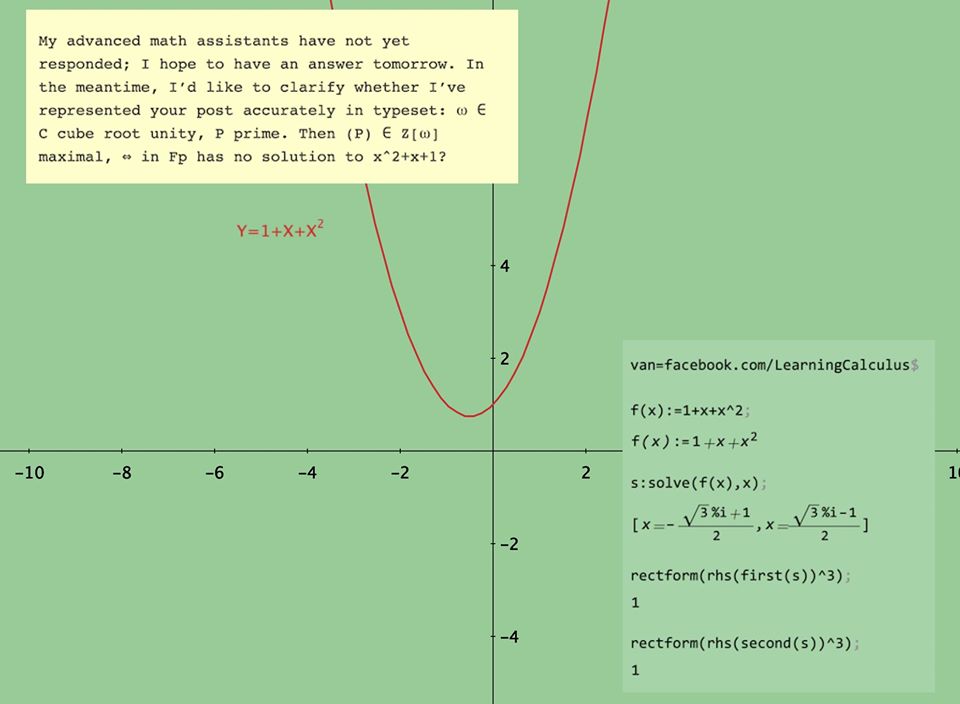
My advanced math assistants have not yet responded; I hope to have an answer tomorrow. In the meantime, I’d like to clarify whether I’ve represented your post accurately in typeset: ω ∈ C cube root unity, P prime. Then (P) ∈ Z[ω] maximal, ⇔ in Fp has no solution to x^2+x+1?
Update 12/5: My assistants had to travel many moons and across many mountains to find a wise person who could answer this question. Here is his answer: The notation to me asks, “We are looking for solutions omega, in the complex plane that satisfy the polynomial P and want to know if they are, or are not deMoivre numbers, that is, complex numbers that when raised to an integer power (in this case 3 from the cube root) produce the value of 1. Both roots of this polynomial satisfy this as I have shown. I’m not sure by Fp, whether they are referring to the function space of polynomials, the antiderivative, the derivative or a field relationship. I’m also not sure what they are looking for with respect to the prime constraint, all the coefficients are 1, 1 is defined NOT to be prime so I’m not sure how to satisfy that issue. For more info, try this online textbook on Algebraic Number Theory from Stanford U: bit.ly/stanford-number-theory
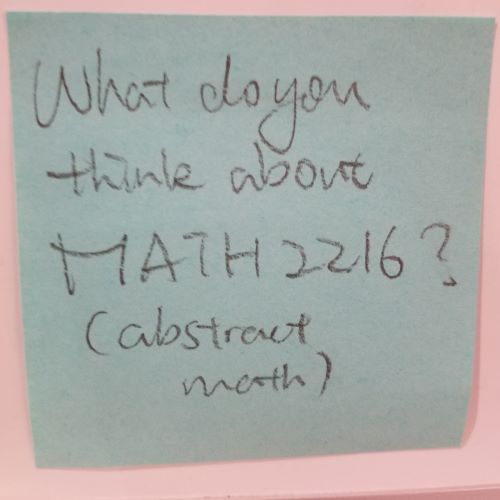
It’s logical. But complex.

It’s not THAT big; why, 1.405 x 10^52 is TEN TIMES bigger! But Douglas Adams was, of course, correct.

I could answer this, but I’m concerned that maybe you can’t, and you need to be able to. How about getting some friendly peer tutoring at the Connors Family Learning Center (bit.ly/BC-connors)?

The Oxford English Dictionary recognizes both as options (and even parameterisation, imagine that!), so you can choose the one you like. I ran a Google Trends search to see usage of the 3 spellings over the past 15 years (bit.ly/Paramewhat); “parameterization” was the clear winner.
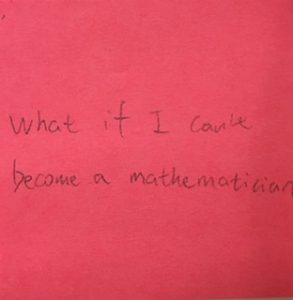
That would be sad, if it’s what your heart is set upon. On the other hand, having a math background will stand you in good stead in anything else you pursue. I recommend the MAA Career Resources Center (bit.ly/MathishCareers) and this site from UC/Irvine (bit.ly/MoreMathCareers). We also have 101 careers in mathematics (O’Neill Stacks QA10.5 .A15 2014). And consider a consultation with the BC Career Center (bit.ly/BC-career). Best of luck!

See the Mathematical Association of America (MAA) Career Resources Center (bit.ly/MathishCareers) for inspiration on what to do with your math degree. Also this site has a lot of information (bit.ly/MoreMathCareers). Or check out the book 101 Careers in Mathematics (O’Neill Stacks QA10.5 .A15 2014). The great thing is that you can bring your math skills to any future path.

This question has been researched thoroughly by parties ranging from high school students to engineering doctorate students. Interestingly enough, results vary drastically. A licking machine (oh yeah, a licking machine!) developed at Purdue University took an average of 364 licks to get to the center of a Tootsie Pop. At the same institution, 20 individuals conducted the same experiment and averaged 252 licks to complete the task. Another licking machine, developed at the University of Michigan required 411 licks to reach the center of a Tootsie Pop; and a group of high school students from Swarthmore Schools averaged 144 licks to achieve the goal So, to answer your question: Getting to the center of a Tootsie Pop takes between 144 to 411 licks, depending on whether you are a teenager or a licking machine.