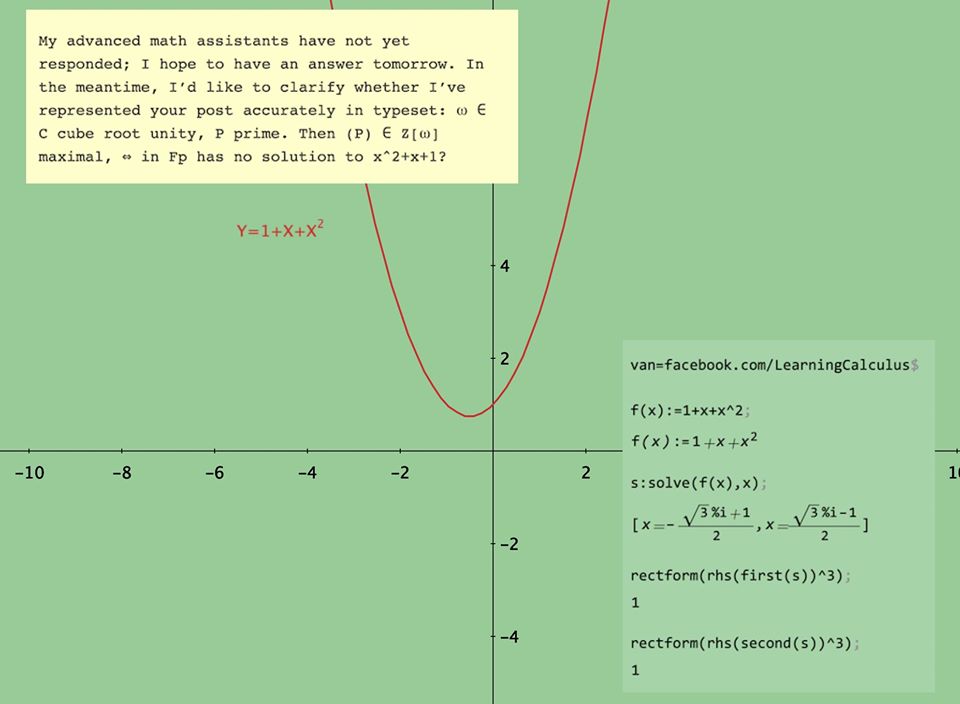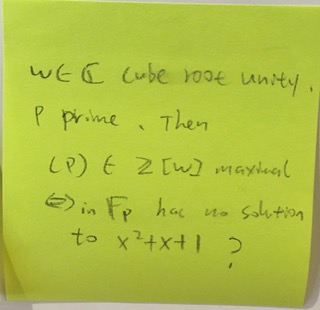
My advanced math assistants have not yet responded; I hope to have an answer tomorrow. In the meantime, I’d like to clarify whether I’ve represented your post accurately in typeset: ω ∈ C cube root unity, P prime. Then (P) ∈ Z[ω] maximal, ⇔ in Fp has no solution to x^2+x+1?
Update 12/5: My assistants had to travel many moons and across many mountains to find a wise person who could answer this question. Here is his answer: The notation to me asks, “We are looking for solutions omega, in the complex plane that satisfy the polynomial P and want to know if they are, or are not deMoivre numbers, that is, complex numbers that when raised to an integer power (in this case 3 from the cube root) produce the value of 1. Both roots of this polynomial satisfy this as I have shown. I’m not sure by Fp, whether they are referring to the function space of polynomials, the antiderivative, the derivative or a field relationship. I’m also not sure what they are looking for with respect to the prime constraint, all the coefficients are 1, 1 is defined NOT to be prime so I’m not sure how to satisfy that issue. For more info, try this online textbook on Algebraic Number Theory from Stanford U: bit.ly/stanford-number-theory